Przedmioty techniczne mają to do siebie, że zawsze dążymy do sprawdzenia poprawności obliczeń. Umożliwiają nam to między innymi różne programy dostępne na rynku. Część jest darmowa, część płatna i bardzo rozbudowana, lecz do naszych celów wystarczy program Statyka dr inż. Adama Zaborskiego. Jest on darmowy i prosty w obsłudze.
Myślę, że samo pobranie i zainstalowanie nie sprawi żadnych problemów, dlatego przejdziemy od razu do omawiania przykładu, bo jeżeli interesuje Cię cała część teoretyczna i wszystkie dostępne opcje odsyłam do plików Pomocy.
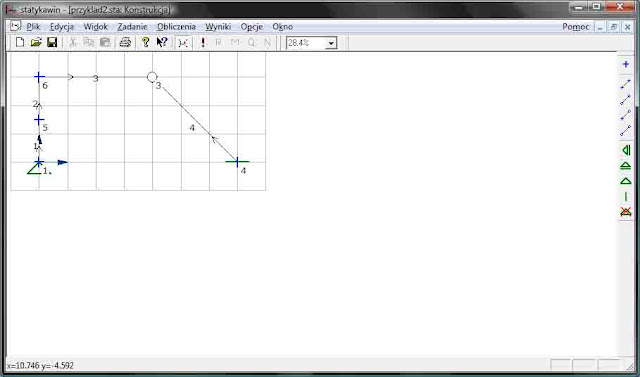
Uruchamiamy program, a naszym oczom ukazuje się taki oto obraz:
Klikamy od razu w pierwszą od lewej ikonkę, aby rozpocząć nowy projekt. Spróbujemy policzyć taką oto ramę:
1. Dodawanie punktów - klikamy na ikonkę + na prawym pasku bocznym i klikamy na siatce tak, aby otrzymać daną geometrię układu. Należy pamiętać, że jeżeli siła występuje na przykład w środku rozpiętości pręta tam również należy dodać punkt, aby móc zdefiniować siłę.
2. Dodawanie prętów i przegubów - 4 ikonki poniżej, pozwalają nam połączyć punkty za pomocą prętów, a dodatkowo umożliwiają dodanie przegubów. Klikamy najpierw w pierwszy punkt, a następnie w kolejny, aby stworzyć połączenie - wszystko intuicyjne. Jedynym problemem może być stworzenie tzw. przegubów podczepionych:
Najpierw musimy stworzyć pręt do którego podczepimy przegub, a dopiero wtedy za pomocą odpowiedniej opcji tworzymy pręt zakończony przegubem, przy innej kolejności powstanie nam zwyczajny przegub.
3. Dodawanie podpór - możemy to wykonać przez pasek szybkiego dostępu po prawej stronie lecz mamy tam tylko 4 najbardziej popularne podpory, w przypadku potrzeby zastosowania innych lub zmiany kąta ustawienia, klikamy prawym przyciskiem myszy na dany punkt i wybieramy polecenie WIĘZY, gdzie mamy wszystkie potrzebne nam opcje.
Ostatecznie powinniśmy otrzymać coś takiego:
Teraz zajmiemy się dodaniem obciążeń. Również możemy zrobić to na dwa sposoby:
1. W przypadku obciążeń skupionych klikamy prawym przyciskiem myszy w dany punkt i wybieramy właściwości punktu. Oprócz możliwości zadania tam odpowiednich sił na kierunku X i Y, możemy tam edytować współrzędne i więzy. W przypadku momentów i obciążeń ciągłych klikamy prawym przyciskiem na dany element i postepujemy analogicznie. Widzimy również, że możemy tam łatwo edytować przeguby.
2. Drugim sposobem jest skorzystanie z menu ZADANIA, w którym są wszystkie potrzebne opcje.
Powinniśmy stworzyć ramę takiego typu:
Możemy teraz przystąpić do najciekawszej części. Klikamy na czerwony wykrzyknik i... błąd. O co chodzi? Jak możemy łatwo sprawdzić jest to zadanie statycznie niewyznaczalne, dlatego nie da się go policzyć tylko za pomocą wcześniej poznanych równań. W przypadku zadań statycznie wyznaczalnych wszystko będzie w porządku i będziemy mogli przejść do dalszych kroków, jednak w tym przypadku musimy dodać jeszcze parę parametrów. Będą one różne w zależności od zadania - w zasadzie zawsze będą podane. Wprowadzimy tutaj standardowe dane i zastosujemy pewna sztuczkę, która zapewni nam wyniki identyczne z naszymi analitycznymi obliczeniami. Klikamy w menu ZADANIA i widzimy dwa polecenia: MATERIAŁ i PRZEKRÓJ. W pierwszym wpisujemy Moduł Young'a - podajemy 1 i klikamy Ustaw dla wszystkich, następnie przechodzimy do drugiego, gdzie Moment bezwładności pozostawiamy z wartością 1, ale Pole przekroju wprowadzamy jako 10000, co da nam pożądane wyniki. Klikamy Ustaw dla wszystkich i ponownie na czerwony wykrzyknik.
Możemy teraz przejść do graficznego wyświetlenia wyników. Pozwala nam na to rozwijalne menu WYNIKI, gdzie mamy szereg opcji. Przykładowo otrzymamy coś takiego:
To by bylo na tyle jeśli chodzi o obliczenia. Jak widzimy bardzo łatwo możemy teraz sprawdzić poprawność naszych ręcznych rachunków.
Na koniec może warto jeszcze wspomnieć o menu OPCJE. Gdzie w menu SKALA mamy często przydatną opcję zmiany skali jednostek wykresu. Dajmy np. 300 % i zobaczmy co się stanie... Kolejną przydatną opcją jest zaznaczenie kwadracika Przyciągaj do siatki w menu SIATKA, co znacznie ułatwi nam rysowanie geometrii układu.
2. Dodawanie prętów i przegubów - 4 ikonki poniżej, pozwalają nam połączyć punkty za pomocą prętów, a dodatkowo umożliwiają dodanie przegubów. Klikamy najpierw w pierwszy punkt, a następnie w kolejny, aby stworzyć połączenie - wszystko intuicyjne. Jedynym problemem może być stworzenie tzw. przegubów podczepionych:
Najpierw musimy stworzyć pręt do którego podczepimy przegub, a dopiero wtedy za pomocą odpowiedniej opcji tworzymy pręt zakończony przegubem, przy innej kolejności powstanie nam zwyczajny przegub.
3. Dodawanie podpór - możemy to wykonać przez pasek szybkiego dostępu po prawej stronie lecz mamy tam tylko 4 najbardziej popularne podpory, w przypadku potrzeby zastosowania innych lub zmiany kąta ustawienia, klikamy prawym przyciskiem myszy na dany punkt i wybieramy polecenie WIĘZY, gdzie mamy wszystkie potrzebne nam opcje.
Ostatecznie powinniśmy otrzymać coś takiego:
Teraz zajmiemy się dodaniem obciążeń. Również możemy zrobić to na dwa sposoby:
1. W przypadku obciążeń skupionych klikamy prawym przyciskiem myszy w dany punkt i wybieramy właściwości punktu. Oprócz możliwości zadania tam odpowiednich sił na kierunku X i Y, możemy tam edytować współrzędne i więzy. W przypadku momentów i obciążeń ciągłych klikamy prawym przyciskiem na dany element i postepujemy analogicznie. Widzimy również, że możemy tam łatwo edytować przeguby.
2. Drugim sposobem jest skorzystanie z menu ZADANIA, w którym są wszystkie potrzebne opcje.
Powinniśmy stworzyć ramę takiego typu:
Możemy teraz przystąpić do najciekawszej części. Klikamy na czerwony wykrzyknik i... błąd. O co chodzi? Jak możemy łatwo sprawdzić jest to zadanie statycznie niewyznaczalne, dlatego nie da się go policzyć tylko za pomocą wcześniej poznanych równań. W przypadku zadań statycznie wyznaczalnych wszystko będzie w porządku i będziemy mogli przejść do dalszych kroków, jednak w tym przypadku musimy dodać jeszcze parę parametrów. Będą one różne w zależności od zadania - w zasadzie zawsze będą podane. Wprowadzimy tutaj standardowe dane i zastosujemy pewna sztuczkę, która zapewni nam wyniki identyczne z naszymi analitycznymi obliczeniami. Klikamy w menu ZADANIA i widzimy dwa polecenia: MATERIAŁ i PRZEKRÓJ. W pierwszym wpisujemy Moduł Young'a - podajemy 1 i klikamy Ustaw dla wszystkich, następnie przechodzimy do drugiego, gdzie Moment bezwładności pozostawiamy z wartością 1, ale Pole przekroju wprowadzamy jako 10000, co da nam pożądane wyniki. Klikamy Ustaw dla wszystkich i ponownie na czerwony wykrzyknik.
Możemy teraz przejść do graficznego wyświetlenia wyników. Pozwala nam na to rozwijalne menu WYNIKI, gdzie mamy szereg opcji. Przykładowo otrzymamy coś takiego:
To by bylo na tyle jeśli chodzi o obliczenia. Jak widzimy bardzo łatwo możemy teraz sprawdzić poprawność naszych ręcznych rachunków.
Na koniec może warto jeszcze wspomnieć o menu OPCJE. Gdzie w menu SKALA mamy często przydatną opcję zmiany skali jednostek wykresu. Dajmy np. 300 % i zobaczmy co się stanie... Kolejną przydatną opcją jest zaznaczenie kwadracika Przyciągaj do siatki w menu SIATKA, co znacznie ułatwi nam rysowanie geometrii układu.